Alexandroff extension

In mathematical field of topology, the Alexandroff extension is a way to extend a noncompact topological space by adjoining a single point in such a way that the resulting space is compact. It is named for the Russian mathematician Pavel Alexandrov.

More precisely, let X be a topological space. Then the Alexandroff extension of X is a certain compact space X* together with an open embedding c : X → X* such that the complement of X in X* consists of a single point, typically denoted ∞. The map c is a Hausdorff compactification if and only if X is a locally compact, noncompact Hausdorff space. For such spaces the Alexandroff extension is called the one-point compactification or Alexandroff compactification. The advantages of the Alexandroff compactification lie in its simple, often geometrically meaningful structure and the fact that it is in a precise sense minimal among all compactifications; the disadvantage lies in the fact that it only gives a Hausdorff compactification on the class of locally compact, noncompact Hausdorff spaces, unlike the Stone–Čech compactification which exists for any Tychonoff space, a much larger class of spaces.

1 Example: inverse stereographic projection
2 Motivation
3 The Alexandroff extension
4 The one-point compactification
5 Further examples
6 See also
7 References

Example: inverse stereographic projection

A geometrically appealing example of one-point compactification is given by the inverse stereographic projection. Recall that the stereographic projection S gives an explicit homeomorphism from the unit sphere minus the north pole (0,0,1) to the Euclidean plane. The inverse stereographic projection 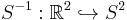$S^{-1}: \mathbb{R}^2 \hookrightarrow S^2$ is an open, dense embedding into a compact Hausdorff space obtained by adjoining the additional point 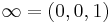$\infty = (0,0,1)$ . Under the stereographic projection latitudinal circles 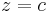$z = c$ get mapped to planar circles 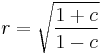$r = \sqrt{\frac{1%2Bc}{1-c}}$ . It follows that the deleted neighborhood basis of 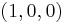$(1,0,0)$ given by the punctured spherical caps $c \leq z < 1$ corresponds to the complements of closed planar disks $r \geq \sqrt{\frac{1%2Bc}{1-c}}$ . More qualitatively, a neighborhood basis at 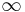$\infty$ is furnished by the sets 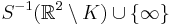$S^{-1}(\mathbb{R}^2 \setminus K) \cup \{ \infty \}$ as K ranges through the compact subsets of 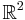$\mathbb{R}^2$ . This example already contains the key concepts of the general case.

Motivation

Let 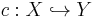$c: X \hookrightarrow Y$ be an embedding from a topological space X to a compact Hausdorff topological space Y, with dense image and one-point remainder 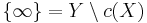$\{ \infty \} = Y \setminus c(X)$ . Then c(X) is open in a compact Hausdorff space so is locally compact Hausdorff, hence its homeomorphic preimage X is also locally compact Hausdorff. Moreover, if X were compact then c(X) would be closed in Y and hence not dense. Thus a space can only admit a one-point compactification if it is locally compact, noncompact and Hausdorff. Moreover, in such a one point compactification the image of a neighborhood basis for x in X gives a neighborhood basis for c(x) in c(X), and—because a subset of a compact Hausdorff space is compact if and only if it is closed—the open neighborhoods of 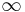$\infty$ must be all sets obtained by adjoining 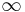$\infty$ to the image under c of a subset of X with compact complement.

The Alexandroff extension

Let X be any topological space, and let 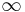$\infty$ be any object which is not already an element of X. (In terms of formal set theory one could take, for example, 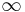$\infty$ to be X itself, but it is not really necessary or helpful to be so specific.) Put 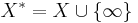$X^* = X \cup \{\infty \}$ , and topologize 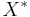$X^*$ by taking as open sets all the open subsets U of X together with all subsets V which contain 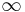$\infty$ and such that 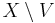$X \setminus V$ is closed and compact, (Kelley 1975, p. 150).

The inclusion map 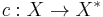$c: X \rightarrow X^*$ is called the Alexandroff extension of X (Willard, 19A).

The above properties all follow easily from the above discussion:

The map c is continuous and open: it embeds X as an open subset of $X^*$ .
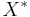The space 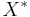$X^*$ is compact.
The image c(X) is dense in 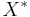$X^*$ , if X is noncompact.
The space 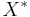$X^*$ is Hausdorff if and only if X is Hausdorff and locally compact.

The one-point compactification

In particular, the Alexandroff extension 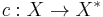$c: X \rightarrow X^*$ is a compactification of X if and only if X is Hausdorff, noncompact and locally compact. In this case it is called the one-point compactification or Alexandroff compactification of X. Recall from the above discussion that any compactification with one point remainder is necessarily (isomorphic to) the Alexandroff compactification.

Let X be any noncompact Tychonoff space. Under the natural partial ordering on the set 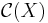$\mathcal{C}(X)$ of equivalence classes of compactifications, any minimal element is equivalent to the Alexandroff extension (Engelking, Theorem 3.5.12). It follows that a noncompact Tychonoff space admits a minimal compactification if and only if it is locally compact.

Further examples

The one-point compactification of the set of positive integers is homeomorphic to the space consisting of K = {0} U {1/n | n is a positive integer.} with the order topology.

The one-point compactification of n-dimensional Euclidean space Rⁿ is homeomorphic to the n-sphere Sⁿ. As above, the map can be given explicitly as an n-dimensional inverse stereographic projection.

Since the closure of a connected subset is connected, the Alexandroff extension of a noncompact connected space is connected. However a one-point compactification may "connect" a disconnected space: for instance the one-point compactification of the disjoint union of $\kappa$ copies of the interval (0,1) is a wedge of $\kappa$ circles.

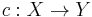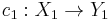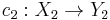The Alexandroff extension can be viewed as a functor from the category of topological spaces to the category whose objects are continuous maps $c: X \rightarrow Y$ and for which the morphisms from $c_1: X_1 \rightarrow Y_1$ to $c_2: X_2 \rightarrow Y_2$ are pairs of continuous maps 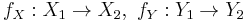$f_X: X_1 \rightarrow X_2, \ f_Y: Y_1 \rightarrow Y_2$ such that 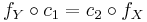$f_Y \circ c_1 = c_2 \circ f_X$ . In particular, homeomorphic spaces have isomorphic Alexandroff extensions.

References

P.S. Alexandroff (1924), "Über die Metrisation der im Kleinen kompakten topologischen Räume", Math. Ann. 92 (3-4): 294–301, doi:10.1007/BF01448011
Ronald Brown (1973), "Sequentially proper maps and a sequential compactification", J. London Math Soc. (2) 7: 515–522

Engelking, Ryszard (1989), General Topology, Helderman Verlag Berlin, ISBN 978-0-201-08707-9, MR 1039321
Fedorchuk, V.V. (2001), "Aleksandrov compactification", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=A/a011260
Kelley, John L. (1975), General Topology, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90125-1, MR 0370454
James Munkres (1999), Topology (2nd ed.), Prentice Hall, ISBN 0-13-181629-2
Willard, Stephen (1970), General Topology, Addison-Wesley, ISBN 3-88538-006-4, MR 0264581